Area between 2 curves calculator

Finding it difficult to calculate the Area between the two curves? Do you want to know about the working of the Area between two curves calculator?

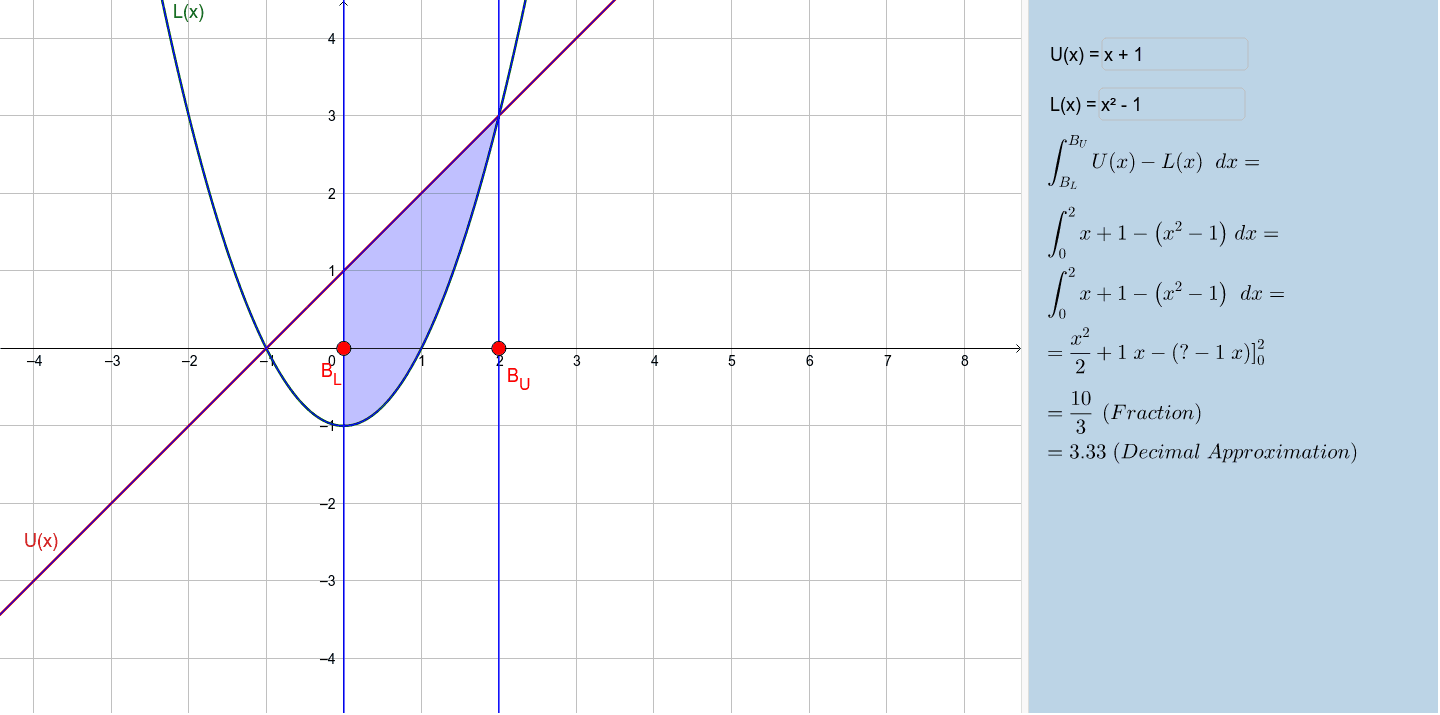
The yellow shaded region in the image below is an example of the area between two curves. This area is a 2-dimensional space bound by the curve of the upper function, the curve of the lower function, a left interval endpoint, and a right interval endpoint. When we first learn about integrals to find the area under a curve, we get our initial insight into the usefulness of calculus for working with complex, real world systems. A basic example of this is using a Riemann Sum to approximate the distance a vehicle traveled by finding the area under its speed versus time curve. But what could we possibly do by finding the area between two curves?

Area between 2 curves calculator

The area between two curves calculator is a free online tool that gives the area occupied within two curves. Step 1: Enter the smaller function, larger function and the limit values in the given input fields. Step 3: Finally, the area between the two curves will be displayed in the new window. The area between two curves can be determined by computing the difference between the definite integrals of two functions. In a two-dimensional geometry, the area is a quantity that expresses the region occupied by the two-dimensional figure. Two functions are required to find the area, say f x and g x , and the integral limits from a to b b should be greater than a of the function, that represent the curve. The area between the two curves is defined as the total region occupied between the two curves in the coordinate plane. If both the curves lie under the x-axis, then the area between two curves will be negative. However, the net signed value is taken as the final answer. The area between the two curves can be calculated by taking absolute difference of the definite integrals between the two functions. Your Mobile number and Email id will not be published. Post My Comment.

If the Integral is negative then is the Area negative too?

To guess, move the cursor on the intersection of the graph on the left The value of z at the intersection which is the lower limit of the integral is stored in Ans and X. This will return to the home screen. Enter the expression to evaluate the integral for the shaded region using the VAR menu and Ans as above. All rights reserved. TI websites use cookies to optimize site functionality and improve your experience. To find out more or to change your preferences, see our cookie policy page. Click Agree and Proceed to accept cookies and enter the site.

The yellow shaded region in the image below is an example of the area between two curves. This area is a 2-dimensional space bound by the curve of the upper function, the curve of the lower function, a left interval endpoint, and a right interval endpoint. When we first learn about integrals to find the area under a curve, we get our initial insight into the usefulness of calculus for working with complex, real world systems. A basic example of this is using a Riemann Sum to approximate the distance a vehicle traveled by finding the area under its speed versus time curve. But what could we possibly do by finding the area between two curves? Well, let's say that we drag race cars at a track on the weekends. Prior to each race, we ensure our data acquisition system inside the vehicle is set to record our speed at set time intervals over the entire duration of each run against our opponent we are racing against. Our opponent also has the same data acquisition system that is recording the same data at the same intervals of time. After each quarter mile race, we would like to know the distance of the gap between our car and our opponent. To do this, we gather the data speed versus time from both cars and find the area between the two speed curves over the entire duration of the quarter mile run in question.

Area between 2 curves calculator

The area between two curves calculator is a free online tool that gives the area occupied within two curves. Step 1: Enter the smaller function, larger function and the limit values in the given input fields. Step 3: Finally, the area between the two curves will be displayed in the new window. The area between two curves can be determined by computing the difference between the definite integrals of two functions. In a two-dimensional geometry, the area is a quantity that expresses the region occupied by the two-dimensional figure.

Mega millions lottery winning numbers

Prior to each race, we ensure our data acquisition system inside the vehicle is set to record our speed at set time intervals over the entire duration of each run against our opponent we are racing against. We may visually determine the upper and lower functions for each subinterval by viewing a graph of the curves. Download as PDF. This will return to the home screen. After solving each area formula integral, we sum the results from each to determine the total area between the curves on our interval. Explore SuperCoaching Now. These cookies help us tailor advertisements to better match your interests, manage the frequency with which you see an advertisement, and understand the effectiveness of our advertising. In other words, by finding the area between these two speed curves, we can determine the distance of the gap between the two vehicles during a specified time interval in the race. These cookies help identify who you are and store your activity and account information in order to deliver enhanced functionality, including a more personalized and relevant experience on our sites. Let us go through some examples to understand the concept better. Well, let's say that we drag race cars at a track on the weekends.

.

If you do not allow these cookies, some or all of the site features and services may not function properly. In some cases, there will only be a single subinterval which is the main interval itself. These cookies help identify who you are and store your activity and account information in order to deliver enhanced functionality, including a more personalized and relevant experience on our sites. Open link in a new tab. How do you determine the area between the two curves? You can control your preferences for how we use cookies to collect and use information while you're on TI websites by adjusting the status of these categories. When we graph a two function on the same xy-plane then we notice that there is some space in between these two curves, the curves might intersect each other or these may not, but if there is space in between two curves in 2-Dimensions then we get the idea of Area. Since the Area is always positive, so we just need to ensure that the final result is positive anyhow irrespective of the integral value. Consider a Rectangular strip of very small width say dx within the given Domain, notice that the height of the Rectangular strip is f x -g x refer the figure below, the part that is coloured in brown. Graphing the functions is an option but it is time consuming, this is not an optimal solution, we have to think in another way.