Differentiation of cos 2x
Derivative differentiation of cos 2x cos 2x is -2 sin 2x which is the process of differentiation of the trigonometric function cos 2x w. It gives the rate of change in cos 2x with respect to angle x. The derivative of cos 2x can be derived using different methods. In this article, differentiation of cos 2x, we will prove the derivative of cos 2x using different methods including the first principle of differentiation and chain rule.
Note that in this post we will be looking at differentiating cos 2 x which is not the same as differentiating cos 2x. Here is our post dealing with how to differentiate cos 2x. The first method is by using the product rule for derivatives since cos 2 x can be written as cos x. The product rule for differentiation states that the derivative of f x. The Product Rule: For two differentiable functions f x and g x. The chain rule is useful for finding the derivative of a function which could have been differentiated had it been in x, but it is in the form of another expression which could also be differentiated if it stood on its own.
Differentiation of cos 2x
The derivative of cos square x is equal to the negative of the trigonometric function sin2x. The derivative of a function gives the rate of change of the function with respect to the variable. In other words, we can also say that the derivative of cos square x gives the function for the slope of the tangent to the function at the points of contact. In this article, we will evaluate the derivative of cos square x and derive its formula using different methods of differentiation including the first principle of derivatives, chain rule, and product rule formula. Generally, we can evaluate this derivative using the chain rule of differentiation which will involve the use of the power rule and the derivative of cos x formula. Other methods to evaluate the derivative of square x are the first principle of derivatives and using the product rule formula. We can evaluate these formulas using various methods of differentiation. Let us go through those derivations in the coming sections. We will use the power rule and the derivative of cos x formula to apply the chain rule to find the derivative of cos square x. So, we have.
Our Mission. Using these facts and formulas, we have.
.
Learn what is the derivative of cos 2x and understand how to prove the derivative of cos 2x by first principle, chain rule and quotient rule. Derivatives have a wide range of applications in almost every field of engineering and science. The derivative of cos 2x can be calculated by following the rules of differentiation. Or, we can directly find the derivative of cos 2x by applying the first principle of differentiation. The derivative of cos 2x with respect to x is -2sin 2x, which tells us how fast the cosine function is changing. In a triangle, the cosine function represents the ratio of the length of the adjacent side to the length of the hypotenuse. By knowing the rate of change of the cosine function, we can analyze the behavior of various systems and make informed decisions.
Differentiation of cos 2x
The derivative of cos square x is equal to the negative of the trigonometric function sin2x. The derivative of a function gives the rate of change of the function with respect to the variable. In other words, we can also say that the derivative of cos square x gives the function for the slope of the tangent to the function at the points of contact. In this article, we will evaluate the derivative of cos square x and derive its formula using different methods of differentiation including the first principle of derivatives, chain rule, and product rule formula. Generally, we can evaluate this derivative using the chain rule of differentiation which will involve the use of the power rule and the derivative of cos x formula. Other methods to evaluate the derivative of square x are the first principle of derivatives and using the product rule formula. We can evaluate these formulas using various methods of differentiation. Let us go through those derivations in the coming sections. We will use the power rule and the derivative of cos x formula to apply the chain rule to find the derivative of cos square x. So, we have.
Venice vaporetto tickets
Maths Puzzles. United States. Example 3: What is the second derivative of cos square x? Kindergarten Worksheets. In this article, we will evaluate the derivative of cos square x and derive its formula using different methods of differentiation including the first principle of derivatives, chain rule, and product rule formula. Already booked a tutor? Terms and Conditions. Already booked a tutor? Derivative of Cos Square x Worksheet. Examples Using Derivative of Cos 2x Examples 1: Find the derivative of cos 2x using the cos 2x formula. The formulas are:. As the name suggests, anti-derivative is the inverse process of differentiation. About Us.
Derivative of cos 2x is -2 sin 2x which is the process of differentiation of the trigonometric function cos 2x w. It gives the rate of change in cos 2x with respect to angle x. The derivative of cos 2x can be derived using different methods.
The Chain Rule: For two differentiable functions f x and g x. Graph of Derivative of Cos 2x 5. The formula for the derivative of cos 2x is:. Maths Puzzles. Anti-Derivative of Cos 2x 6. Here is our post dealing with how to differentiate cos 2x. Now, to evaluate the derivative of cos 2x using the chain rule, we will use certain algebraic and trigonometric properties and identities such as:. Multiplication Tables. So, the derivative of cos square x cube is equal to -3 sin 2x 3. In this article, we will evaluate the derivative of cos square x and derive its formula using different methods of differentiation including the first principle of derivatives, chain rule, and product rule formula. Solution: Derivative of cos 2x is -2 sin 2x. The product rule for differentiation states that the derivative of f x.

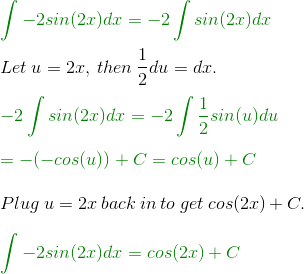
The safe answer ;)
Completely I share your opinion. In it something is and it is good idea. I support you.