Domain and range in a parabola

Given a situation that can be modeled by a quadratic function or the graph of a quadratic function, determine the domain and range of the function.

The domain and range of a function are integral to its definition. In this section, you will learn how to use algebraic techniques to define a function's domain and range given its equation. The general form of a quadratic function presents the function in the form where , and are real numbers and. If , the parabola opens upward. If , the parabola opens downward. We can use the general form of a parabola to find the equation for the axis of symmetry.

Domain and range in a parabola

If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Search for courses, skills, and videos. Determining the range of a function Algebra 2 level. About About this video Transcript. Want to join the conversation? Log in. Sort by: Top Voted. Posted 11 years ago. Downvote Button navigates to signup page. Flag Button navigates to signup page. Show preview Show formatting options Post answer. Sal mentions how to find the vertex at Comment Button navigates to signup page. Should I take the Quadratics course before Functions?

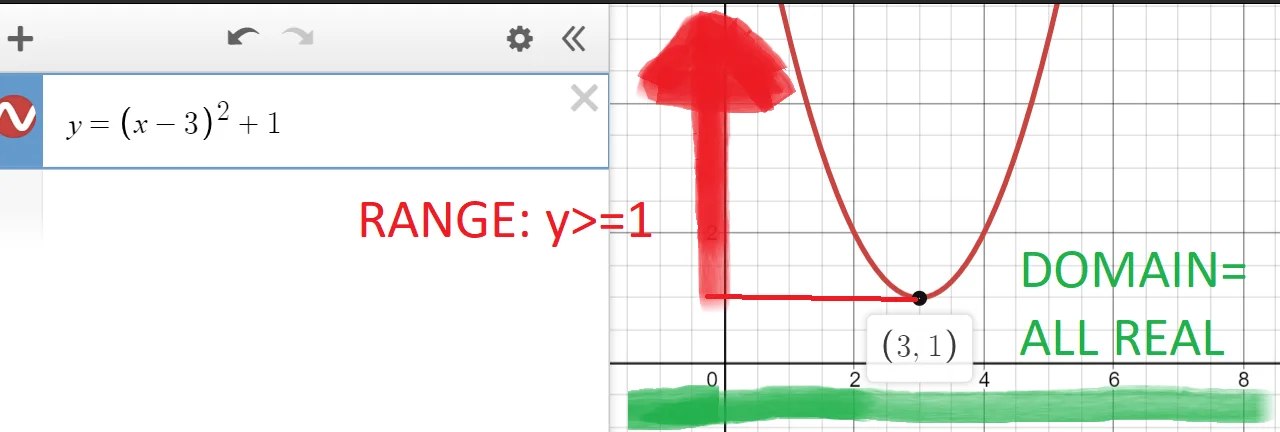
Determine the domain and range of the function, and check to see if you interpreted the graph correctly.

There are four different common relationships between variables you're sure to run into: they're linear, direct, quadratic, and inverse relationships. Here, we'll go over both quadratic relationships, and a couple of examples of finding domain and range of a quadratic function. Fun explodes with the solving of equations, making graphs along with understanding the real-life and practical use of this function. And one of its important characteristics is how to find the domain and range of a quadratic function or domain and range of a parabola in other words. In many places, you'll encounter a quadratic relation in physics with projectile motion.

A Quadratic Function is any function defined by a polynomial whose greatest exponent is two. The graph of any quadratic function is a U-shaped curve called a parabola. There are certain key features that are important to recognize on a graph and to calculate from an equation. Definitions: Forms of Quadratic Functions. A quadratic function is a polynomial function of degree two. The graph of a quadratic function is a parabola. A formula for the location of the vertex for a quadratic in general form can be found by equating the two forms for a quadratic. How features of the parabola for a quadratic function can be obtained is summarized below. Knowing that the vertex of a parabola is the lowest or highest point of the parabola gives us an easy way to determine the minimum or maximum value of a quadratic function. Therefore, the domain of any quadratic function is all real numbers.

Domain and range in a parabola

The cross-section of the antenna is in the shape of a parabola, which can be described by a quadratic function. In this section, we will investigate quadratic functions, which frequently model problems involving area and projectile motion. Working with quadratic functions can be less complex than working with higher degree functions, so they provide a good opportunity for a detailed study of function behavior. The graph of a quadratic function is a U-shaped curve called a parabola.

Target return policy prepaid cell phones

Because the vertex appears in the standard form of the quadratic function, this form is also known as the vertex form of a quadratic function. The maximum value is given by. And, if you're familiar with quadratics-- and that's what this function is right over here, it is a quadratic-- you might already know that it has a parabolic shape. Our range, the possible y values is all real numbers greater than or equal to negative 5. Identify the domain of any quadratic function as all real numbers. The standard form of a quadratic function prior to writing the function then becomes the following:. Q What makes the function quadratic? Course Feedback Survey. Determine the domain and range of the function, and check to see if you interpreted the graph correctly. This equation is in a factored form. Then find the vertical coordinate of the vertex. The range is all y values. Since in this example,. But the parabola has a vertex which is a minimum y-value for any parabola that faces up or a maximum y-value for any parabola that faces down.

To find out more about why you should hire a math tutor, just click on the "Read More" button at the right! When working with a parabola, you may need to know the possible inputs domain, or x-values and outputs range, or y-values. This will involve finding the local minimum or maximum vertex , along with figuring out concavity of the parabola.

Figure 4 The standard form of a quadratic function presents the function in the form where is the vertex. Or, we should go from negative 5 all the way to positive 7. Example 2. So, it would look something, something like that, and keep on going in that direction. I could keep going, this is in the y, and we're going to set y equal to whatever our output of the function is. Example 4. And, this is where you can see that this is the vertex, and you start seeing the symmetry. But the range of a parabola is a little trickier. Rewrite the quadratic in standard form vertex form. Figure 5 represents the graph of the quadratic function written in standard form as. The bottom is positive, but again, getting closer and closer to 0. Determine the domain and range of the function, and check to see if you interpreted the graph correctly. This makes the analysis much simpler. The axis of symmetry is defined by.