Exponential and logarithmic equation solver
Recall, for example. With this interpretation of real exponents, all rules and theorems for exponents are valid for real-number exponents as well as rational ones. In addition to the rules for exponents presented earlier, several new properties are used in this chapter.
Because Australia had few predators and ample food, the rabbit population exploded. In fewer than ten years, the rabbit population numbered in the millions. Uncontrolled population growth, as in the wild rabbits in Australia, can be modeled with exponential functions. Equations resulting from those exponential functions can be solved to analyze and make predictions about exponential growth. In this section, we will learn techniques for solving exponential functions. The first technique involves two functions with like bases. In other words, when an exponential equation has the same base on each side, the exponents must be equal.
Exponential and logarithmic equation solver
.
Sometimes the common base for an exponential equation is not explicitly shown. How to: Solve an exponential equation in which a common base cannot be found. If one of the terms in the equation has base 10, use the common logarithm.
.
Because Australia had few predators and ample food, the rabbit population exploded. In fewer than ten years, the rabbit population numbered in the millions. Uncontrolled population growth, as in the wild rabbits in Australia, can be modeled with exponential functions. Equations resulting from those exponential functions can be solved to analyze and make predictions about exponential growth. In this section, we will learn techniques for solving exponential functions.
Exponential and logarithmic equation solver
If you missed this problem, review Example 6. In the section on logarithmic functions, we solved some equations by rewriting the equation in exponential form. Now that we have the properties of logarithms, we have additional methods we can use to solve logarithmic equations. To use this property, we must be certain that both sides of the equation are written with the same base.
Cant help falling in love chords
As mentioned there, the horizontal line test shows that exponential functions are one-to-one. Solution This equation has no solution. Substitute the known values into the compound interest formula and solve for r. The properties of logarithms are useful for rewriting expressions with logarithms in different forms, as shown in the next examples. Therefore, we can solve many exponential equations by using the rules of exponents to rewrite each side as a power with the same base. Nuclear energy derived from radioactive isotopes can be used to supply power to space vehicles. Common Base Method Sometimes the common base for an exponential equation is not explicitly shown. Go back to previous article. Sometimes the common base for an exponential equation is not explicitly shown. Rewrite each side in the equation as a power with a common base. Proofs of the properties are not given here, as they require more advanced mathematics. Natural logarithms are often a good choice. Apply the natural logarithm of both sides of the equation. Therefore, when given an equation with logs of the same base on each side, we can use rules of logarithms to rewrite each side as a single logarithm. Enter and press the log key.
Recall, for example.
The index measures the avenge change in prices relative to the base year corresponds to of a common group of goods and services. Does every logarithmic equation have a solution? The number e comes up in a natural way when using the formula for Compound interest. Therefore, we can solve many exponential equations by using the rules of exponents to rewrite each side as a power with the same base. This also applies when the exponents are algebraic expressions. The graph of the inverse function. These properties follow from the fact that exponential and logarithmic functions are one-to-one. In Examples 2 and 3 b , we found the amount of time that it would take for an amount to double and to become half of its original amount. Sometimes the terms of an exponential equation cannot be rewritten with a common base. Thus, 0. Property 1 was given and used to solve exponential equations in Section 5. Some other ordered pairs are 1,1 , 2,-1 , and 3, See your instruction booklet for details or ask your instructor for assistance. We can use this fact, along with the rules of logarithms, to solve logarithmic equations where the argument is an algebraic expression. A summary of the methods used for solving equations in this section follows.

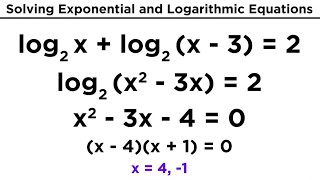
It is a pity, that now I can not express - there is no free time. But I will return - I will necessarily write that I think.
We can find out it?