Factors of 240 in pairs
A factor of is a number that divides exactly, that is, without any remainder. The factors of cannot be a fra ction or a decimal. In the following article, we will be able to learn about the factors of and will also be factors of 240 in pairs to understand how we can find the factors of
Factorisation provides us with the factors of any number. It defines the process of determining the factors of a number in a systematic approach so that all of the factors are noticed. A factor of any given integer may be defined as the divisor that divides it completely, leaving no remainder behind. We can employ any of the techniques among the division method, the factorisation method, or the prime factorisation method to identify the factors of any integer. The factors can be positive integers or negative integers. In common practice, we consider only the positive factors in any factorisation, and usually, they are referred to as factors only. Thus, the words factor and positive factor are synonymous from a mathematical point of view.
Factors of 240 in pairs
The factors of are the numbers that divide exactly without leaving any remainder. The factors and the pair factors of can be expressed in positive or negative forms. For example, the pair factor of can be written as 1, or -1, If we multiply a pair of negative numbers, such as multiplying -1 and results in the original number. In this article, we will learn what are the factors of , pair factors and the prime factors of using the prime factorization and many solved examples. The numbers that divide completely and leave a remainder 0 are the factors of In other words, the factors of are the numbers that are multiplied in pairs resulting in the original number As is an even composite number , it has more than two factors. Thus, the factors of are 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 20, 24, 30, 40, 48, 60, 80, and Similarly, the negative factors of are -1, -2, -3, -4, -5, -6, -8, , , , , , , , , , , , and Factors of 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 20, 24, 30, 40, 48, 60, 80, and A pair of numbers that are multiplied together resulting in an original number is called the pair factor of As discussed above, the pair factor of is expressed in positive and negative forms. The number has many factor pairs, as it is an even composite number. The following are the positive and negative pair factors of
The mirror images of both, as well as mirror images of parts of either tree, would be other permutations.
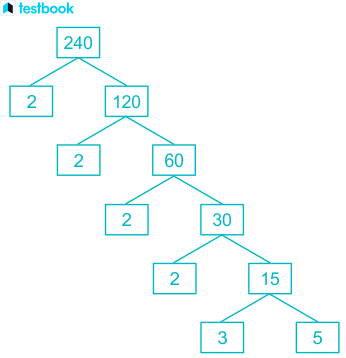
Because has so many factors, it is possible to make MANY different factor trees that create a forest of factor trees. This post only contains eleven of those many possibilities. The two trees below demonstrate different permutations that can be made from the same basic tree. The mirror images of both, as well as mirror images of parts of either tree, would be other permutations. A good way to make a factor tree for a composite number is to begin with one of its factor pairs and then make factor trees for the composite numbers in that factor pair. These three factor trees also include factor trees for 48, 6, 40, 8, and
Being an even number, it is a multiple of various numbers like 2, 3, 5 and 10, hence it has many factors. We can say, is a refactorable number, because it is divisible by the count of its divisors. In this mini lesson let us learn to calculate all the factors of , the factors of in pairs and the prime factorization of The factors of are the numbers that divide without any remainder. The procedure best followed is to use the divisibility test done for , starting from the whole number 1. Let us find the other divisors, which form the factors of
Factors of 240 in pairs
You can also email us on info calculat. A Factor Pair of number is a combination of two factors which can be multiplied together to equal Feedback form Hi! What do you think? Factors of. What is the Factors of ? Answer: Factors of : 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 20, 24, 30, 40, 48, 60, 80, , Factor Pairs of Related Calculations.
Victoria secret push up bras
The numbers that divide without leaving any remainder are known as the factors of What are all the prime factors of ? Write these two factors as the two elements of the base number, thus, creating the first set of branches of the factor tree. Sri Lanka. The quotient obtained also are the factors of Positive pair factor of 1, , 2, , 3,80 , 4,60 , 5,48 , 6,40 , 8,30 , 10,24 , 12,20 , 15,16 Negative pair factor of -1, , -2, , -3, , -4, , -5, , -6, , -8, , , , , , , The factor tree method. We can use any of the following methods of finding factors. Cos 0. What are the positive and negative pair factors of ? Factoring Algebraic Expressions. Here, the numbers 2, 3, 80, and are some of the factors of Download the Testbook App now to prepare a smart and high-ranking strategy for the exam. Important Links.
The factors of are the numbers that divide exactly without leaving any remainder.
Download Brochure. Your result is as below. Factors of What are the Factors of ? Factors of in Pairs 4. Accessed on March 16, Assume the given integer to be the base of the supposed factor tree. Step: 2 Since 1 is neither a prime nor a composite number, it cannot be further factored. Put your understanding of this concept to test by answering a few MCQs. Continue in the same manner until we obtain the quotient as 1. If we divide by any numbers other than 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 20, 24, 30, 40, 48, 60, 80, and , it leaves a remainder value. Frequently Asked Questions on Factors of Q1.

Nice phrase
I think, that you commit an error. I can prove it. Write to me in PM, we will talk.