In a parallelogram opposite angles are equal

If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Search for courses, skills, and videos. Theorems concerning quadrilateral properties.

Measurement and Geometry : Module 20 Years : PDF Version of module. In contrast, there are many categories of special quadrilaterals. Apart from cyclic quadrilaterals, these special quadrilaterals and their properties have been introduced informally over several years, but without congruence, a rigorous discussion of them was not possible. Each congruence proof uses the diagonals to divide the quadrilateral into triangles, after which we can apply the methods of congruent triangles developed in the module, Congruence. The material in this module is suitable for Year 8 as further applications of congruence and constructions.

In a parallelogram opposite angles are equal

The properties of a parallelogram help us to identify a parallelogram from a given set of figures easily and quickly. Before we learn about the properties, let us first know about parallelograms. It is a four-sided closed figure with equal and parallel opposite sides and equal opposite angles. Let us learn more about the properties of parallelograms in detail in this article. A parallelogram is a type of quadrilateral in which the opposite sides are parallel and equal. There are four angles in a parallelogram at the vertices. Understanding the properties of parallelograms helps to easily relate its angles and sides. Also, the properties are helpful for calculations in problems relating to the sides and angles of a parallelogram. All the above properties hold true for all types of parallelograms, but now let us also learn about the individual properties of some special parallelograms. The three different parallelograms are square, rectangle, and rhombus which are different from each other because of their properties yet they all come under the category of parallelograms. Now, let us expand our knowledge by learning about the properties of diagonals of parallelograms in the following section.. First, we will recall the meaning of a diagonal. Diagonals are line segments that join the non-adjacent vertices of any polygon. The properties of diagonals of a parallelogram are as follows:.

United States. If a parallelogram is known to have one right angle, then repeated use of co-interior angles proves that all its angles are right angles. Theorems about special quadrilaterals will be widely used in coordinate geometry.

The opposite angles of a parallelogram are equal and the consecutive angles of a parallelogram are supplementary. Let us read more about the properties of the angles of a parallelogram in detail. A parallelogram is a quadrilateral with equal and parallel opposite sides. There are some special properties of a parallelogram that make it different from the other quadrilaterals. Observe the following parallelogram to relate to its properties given below:.

A Quadrilateral has four-sides , it is 2-dimensional a flat shape , closed the lines join up , and has straight sides. Also see this on Interactive Quadrilaterals. Try drawing a quadrilateral, and measure the angles. Some types are also included in the definition of other types! For example a square , rhombus and rectangle are also parallelograms. See below for more details.

In a parallelogram opposite angles are equal

The properties of a parallelogram help us to identify a parallelogram from a given set of figures easily and quickly. Before we learn about the properties, let us first know about parallelograms. It is a four-sided closed figure with equal and parallel opposite sides and equal opposite angles. Let us learn more about the properties of parallelograms in detail in this article.

Old packaging of jollibee

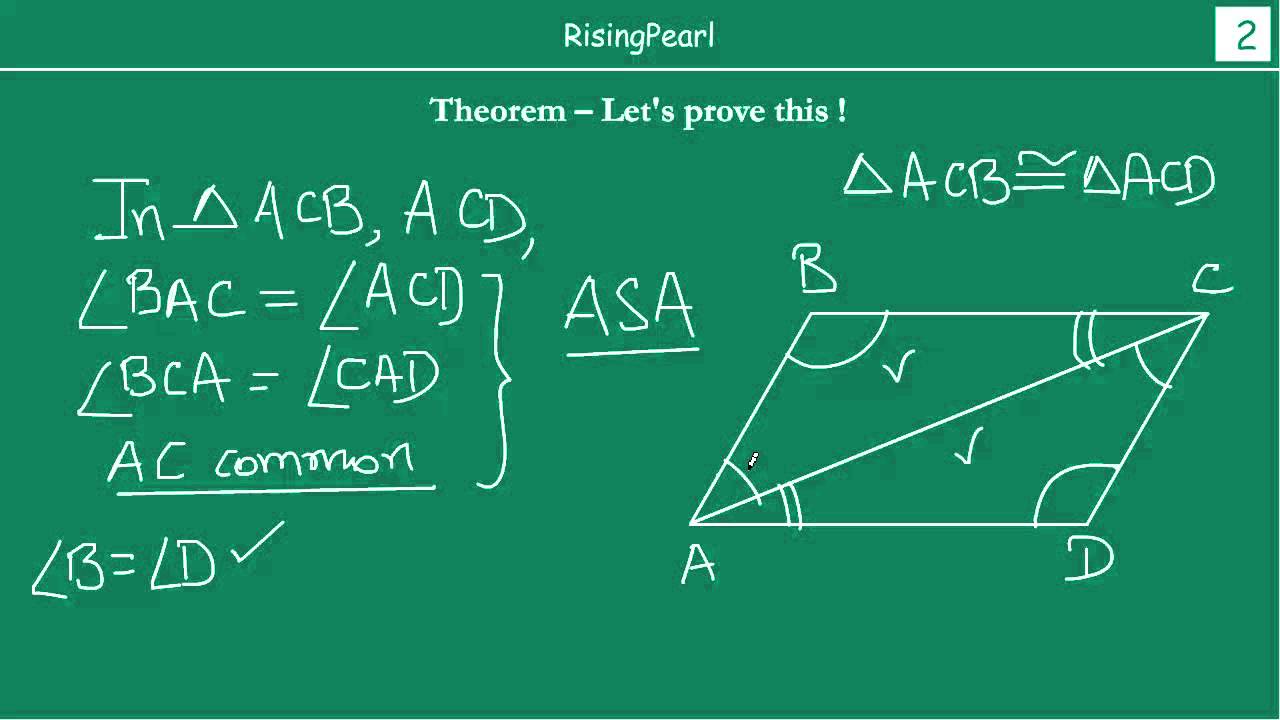
United States. Saudi Arabia. The next step in the development of geometry is a rigorous treatment of similarity. Hence by the ASA criterion, both the triangles are congruent and the corresponding sides are equal. Theorems on Parallelogram Properties 4. Would it be equally acceptable to use a plain equals sign instead? The remaining special quadrilaterals to be treated by the congruence and angle-chasing methods of this module are rhombuses, kites, squares and trapezia. Before we learn about the properties, let us first know about parallelograms. For example, the fact that the base angles of an isosceles triangle are equal is a property of isosceles triangles. This means that a rectangle is a parallelogram, so:. The consecutive angles of a parallelogram are supplementary. The first property is most easily proven using angle-chasing, but it can also be proven using congruence. No, according to the theorems based on the angles of a parallelogram, the opposite angles are not supplementary, they are equal. We begin with parallelograms, because we will be using the results about parallelograms when discussing the other figures.

A parallelogram is a quadrilateral in which the opposite sides are parallel and equal. Parallelograms are classified into three main types: square, rectangle, and rhombus, and each of them has its own unique properties. In this article, let us learn about the parallelogram shape , the parallelogram definition , the different types of parallelograms , how to find the area of a parallelogram and parallelogram examples.

Terms and Conditions. There are four angles in a parallelogram at the vertices. See the module, Construction. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. And the parallel lines and the transversals actually switch roles. In short, a parallelogram can be considered a twisted rectangle. If not, when would you use a congruent symbol and when would you use an equals sign to compare angles? Because ABCD is a parallelogram, its opposite sides are equal. Math will no longer be a tough subject, especially when you understand the concepts through visualizations. Gyung-chae Han. Direct link to Antheni M.