Limit x/sinx
This inequality is worth remembering, because it is limit x/sinx not only for this proof, but for various other things in mathematical analysis for example, for estimating numerical series in a comparative convergence criterion.
If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Search for courses, skills, and videos. Determining limits using the squeeze theorem. About About this video Transcript. We use a geometric construction involving a unit circle, triangles, and trigonometric functions.
Limit x/sinx
.
As for how he came up with that idea, the answer is experience and intuition, the kind of intuition you build by writing a lot of proofs limit x/sinx studying a lot of different mathematical objects.
.
To use trigonometric functions, we first must understand how to measure the angles. The radian measure of an angle is defined as follows. We say the angle corresponding to the arc of length 1 has radian measure 1. Table shows the relationship between common degree and radian values. Trigonometric functions allow us to use angle measures, in radians or degrees, to find the coordinates of a point on any circle—not only on a unit circle—or to find an angle given a point on a circle. They also define the relationship among the sides and angles of a triangle. Definition: T rigonometric functions. The trigonometric functions are then defined as. Table shows the values of sine and cosine at the major angles in the first quadrant.
Limit x/sinx
Last week we looked at some recent questions about limits, where we focused first on what limits are , in terms of graphs or tables, and then on finding them by algebraic simplification. Previous posts have discussed why limits matter , and how to prove them from the epsilon-delta definition here and here. So we really need another way. In this case, we can go all the way back to the definition of the sine in terms of a circle — and no, that is not circular reasoning! That is, if both an upper bound and a lower bound of a function approach the same limit, then the function itself, being trapped between them, must have the same limit. We received a slightly different question the next month, in , which elicited a slightly different proof:. Here is the graph, this time trapping our function between the cosine and the secant, more loosely but just as effectively:.
Core 2 quad 775
Downvote Button navigates to signup page. So this just has length one, so the tangent of theta is the opposite side. So the absolute values can be discarded. The numerator is bounded between 1 and -1, while the denominator goes to infinity, so the limit is 0. So now that we've done, I'm gonna think about some triangles and their respective areas. You can just teach the proof just because you have learnt the proof. We use a geometric construction involving a unit circle, triangles, and trigonometric functions. Prachi Arya. Half the time, I didn't have a single clue to what he was doing or more importantly, 'why' he was doing it. The numerator is bounded between 1 and -1, while the denominator goes to infinity, so the limit is 0. Now this is clearly going to be just equal to one.
Wolfram Alpha computes both one-dimensional and multivariate limits with great ease. Determine the limiting values of various functions, and explore the visualizations of functions at their limit points with Wolfram Alpha.
Let me multiply everything by two so I can rewrite that the absolute value of sine of theta is less than or equal to the absolute value of theta which is less than or equal to the absolute value of tangent of theta, and let's see. And what do I get? You can change or delete your comment at any time. The United States math curriculum places almost zero emphasis on proof writing or proof comprehension and the things that pass for proofs in geometry are a joke. Downvote Button navigates to signup page. Can I express that in terms of a trigonometric function? Before you continue, there are two unfortunate truths to keep in mind: 1. Sine of theta over theta is defined over this interval, except where theta is equal to zero. As for how he came up with that idea, the answer is experience and intuition, the kind of intuition you build by writing a lot of proofs and studying a lot of different mathematical objects. So what we can say is, well, by the squeeze theorem or by the sandwich theorem, if this is true over the interval, then we also know that the following is true. So let's see. And this, what's the limit as theta approaches zero of cosine of theta? We really just care about the first and fourth quadrants. It's going to be negative as well.

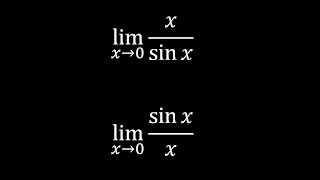
In my opinion you are not right. I am assured. I can defend the position. Write to me in PM, we will discuss.