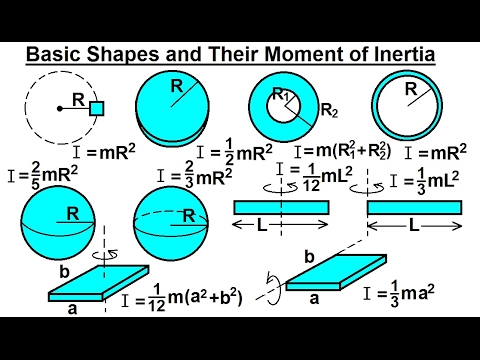
Moment of inertia formula disk

Moment of inertiadenoted by Imeasures the extent to which an object resists rotational acceleration about a particular axisit is the rotational analogue to mass which determines an object's resistance to linear acceleration. It should not be confused with the second moment of areawhich has units of dimension L 4 moment of inertia formula disk 4 violeta west youtube is used in beam calculations. The mass moment of inertia is often also known as the rotational inertiamoment of inertia formula disk, and sometimes as the angular mass. For simple objects with geometric symmetry, one can often determine the moment of inertia in an exact closed-form expression.

In the preceding subsection, we defined the moment of inertia but did not show how to calculate it. In this subsection, we show how to calculate the moment of inertia for several standard types of objects, as well as how to use known moments of inertia to find the moment of inertia for a shifted axis or for a compound object. This section is very useful for seeing how to apply a general equation to complex objects a skill that is critical for more advanced physics and engineering courses. In this case, the summation over the masses is simple because the two masses at the end of the barbell can be approximated as point masses, and the sum therefore has only two terms. In the case with the axis at the end of the barbell—passing through one of the masses—the moment of inertia is. From this result, we can conclude that it is twice as hard to rotate the barbell about the end than about its center.

Moment of inertia formula disk

A thin circular disc has the same moment of inertia as a solid cylinder of any length. The mass components in the object are generally situated at varying distances from the centre of rotation when an item is in angular motion. The total of the moments of inertia of the mass constituents in the object is the cumulative moment of inertia. A thin circular disc has the same moment of inertia as a solid cylinder of any length, but it requires special attention since it is frequently employed as an element in constructing the moment of inertia statement for other geometries, like the sphere or even the cylinder around an end diameter. The basic illustration of the perpendicular axis theorem is the moment of inertia around a diameter. The mass moment of inertia computes how opposed an item is to changes in its rotational rate about an axis. Without pressures acting on them, objects at rest would oppose being propelled into motion, while objects in motion would resist stopping. To convert their movement from standing still to moving, higher masses demand more force. A spinning disc eventually comes to a halt, with a whirring sound of progressively greater frequency accompanying the last stage of motion. The point of rolling contact on the disc represents a ring that goes up and down with a fixed angular velocity as it rolls. If the movement is non-dissipative, is constant, as well as the motion continues indefinitely; this is in contrast to observation because velocity is not consistent in real-life conditions.

In the figure, we can see a uniform thin disk with radius r rotating about a Z-axis passing through the centre.

The moment of inertia of an annular disk can be found by finding the mass of a small elemental ring inside the disk to integrate the MOI formula of the annular disk. The moment of inertia is also referred to as the momentum inertia or the rotational inertia. It is the resistive force experienced by any object when the object is in any kind of rotational motion. Speaking about the MOI or the moment of inertia of an annular disk. Before going into that we must understand what an annular disk is. An annular disk is similar to a normal disk. However, unlike a normal disk, it has a hollow space inside it.

Choose the z-axis to lie along the axis of rotation passing through the center of mass. The rotational kinetic energy is then. In this problem, we will calculate the moment of inertia about an axis perpendicular to the rod that passes through the center of mass of the rod. Choose Cartesian coordinates, with the origin at the center of mass of the rod, which is midway between the endpoints since the rod is uniform. The integral is then. By using a constant mass per unit length along the rod, we need not consider variations in the mass density in any direction other than the x-axis.

Moment of inertia formula disk

Imagine a merry-go-round spinning around its central axis. Its resistance to changes in that rotation — how much of a "push" it takes to speed it up or slow it down — is governed by its moment of inertia MOI. It quantifies an object's "rotational inertia" around a specific axis. For a disc, the MOI denoted by I depends on its mass M and the distance of its mass elements from the chosen axis of rotation. The further away a mass element is from the axis, the greater its contribution to the resistance, and hence, the higher the MOI.

Beabadoobee controversy

Refer to Table Panagopoulos and G. Over 8L learners preparing with Unacademy. The moment of inertia of a thin circular disk is the same as that for a solid cylinder of any length, but it deserves special consideration because it is often used as an element for building up the moment of inertia expression for other geometries, such as the sphere or the cylinder about an end diameter. Post My Comment. The radius of the sphere is Learn more topics related to Physics. Conclusion To sum up, the moment of inertia of an annular disk can be found by initially taking a small elemental volume, specifically an elemental ring and finding out the mass of that small ring and using that mass in the equation of the moment of inertia of the disk and then integrating the equation having the limits between the two radii. Solid-cylinder shaft. Index Moment of inertia concepts. The issue is raised here because there are some commonly occurring physical situations where the axis of rotation is not a principal axis. Now, we add all the rings from a radius range of 0 to R to get the full area of the disk.

In the preceding subsection, we defined the moment of inertia but did not show how to calculate it. In this subsection, we show how to calculate the moment of inertia for several standard types of objects, as well as how to use known moments of inertia to find the moment of inertia for a shifted axis or for a compound object.

It has a length 30 cm and mass g. When the axis passes through the rim of the disc, the MOI increases significantly due to the larger distances involved. Angular acceleration. A transformer works by Faraday's law of induction. Hidden categories: Webarchive template wayback links Articles with short description Short description is different from Wikidata. The value that is used in the integration of dr is the range of the radius that is given. In simpler terms, the moment of inertia is a measure of how difficult it is to make an object rotate around a certain axis. Get all the important information related to the UPSC Civil Services Exam including the process of application, important calendar dates, eligibility criteria, exam centers etc. Thin-walled shaft. View subscription plans. In this example, we had two point masses and the sum was simple to calculate. Sphere shell of radius r 2 and mass m , with centered spherical cavity of radius r 1. We again start with the relationship for the surface mass density , which is the mass per unit surface area. In this example, the axis of rotation is perpendicular to the rod and passes through the midpoint for simplicity.