Positive real numbers
Real numbers are simply the combination of rational and irrational numbers, in the number system.
Wiki User. Natural numbers extend from 1 to positive infinity. Real numbers are all numbers between negative infinity and positive infinity. When two negative real numbers are multiplied together, the product is a positive real number. Real numbers include positive and negative numbers, integers and fractions, rational and irrational numbers. Real numbers include fractional and decimal numbers.
Positive real numbers
This ray is used as reference in the polar form of a complex number. It inherits a topology from the real line and, thus, has the structure of a multiplicative topological group or of an additive topological semigroup. In the study of physical magnitudes, the order of decades provides positive and negative ordinals referring to an ordinal scale implicit in the ratio scale. Among the levels of measurement the ratio scale provides the finest detail. The division function takes a value of one when numerator and denominator are equal. Other ratios are compared to one by logarithms, often common logarithm using base The ratio scale then segments by orders of magnitude used in science and technology, expressed in various units of measurement. An early expression of ratio scale was articulated geometrically by Eudoxus : "it was In the context of topological groups, this measure is an example of a Haar measure. The utility of this measure is shown in its use for describing stellar magnitudes and noise levels in decibels , among other applications of the logarithmic scale. For purposes of international standards ISO , the dimensionless quantities are referred to as levels.
This uniqueness allows us to think of them as essentially the same mathematical object. Complex conjugate Complex plane Imaginary number Real number Unit complex number. All these definitions satisfy the axiomatic definition and are thus equivalent.
In mathematics , a real number is a number that can be used to measure a continuous one- dimensional quantity such as a distance , duration or temperature. Here, continuous means that pairs of values can have arbitrarily small differences. The real numbers are fundamental in calculus and more generally in all mathematics , in particular by their role in the classical definitions of limits , continuity and derivatives. The rest of the real numbers are called irrational numbers. Real numbers can be thought of as all points on a line called the number line or real line , where the points corresponding to integers Conversely, analytic geometry is the association of points on lines especially axis lines to real numbers such that geometric displacements are proportional to differences between corresponding numbers.
A subset is a set consisting of elements that belong to a given set. When studying mathematics, we focus on special sets of numbers. Notice that the sets of natural and whole numbers are both subsets of the set of integers. Decimals that repeat or terminate are rational. For example,. Irrational numbers are defined as any number that cannot be written as a ratio of two integers.
Positive real numbers
This ray is used as reference in the polar form of a complex number. It inherits a topology from the real line and, thus, has the structure of a multiplicative topological group or of an additive topological semigroup. In the study of physical magnitudes, the order of decades provides positive and negative ordinals referring to an ordinal scale implicit in the ratio scale.
Ocean grove hair salon
All Rights Reserved. Is the real number a subset of a complex number? Here, continuous means that pairs of values can have arbitrarily small differences. One can use the defining properties of the real numbers to show that a is the least upper bound of the D n. Retrieved Real numbers. In the physical sciences, most physical constants such as the universal gravitational constant, and physical variables, such as position, mass, speed, and electric charge, are modeled using real numbers. Log in. Elements of Baire space are referred to as "reals". Complex conjugate Complex plane Imaginary number Real number Unit complex number.
Real numbers are simply the combination of rational and irrational numbers, in the number system. In general, all the arithmetic operations can be performed on these numbers and they can be represented in the number line, also.
The Middle Ages brought about the acceptance of zero , negative numbers , integers, and fractional numbers, first by Indian and Chinese mathematicians , and then by Arabic mathematicians , who were also the first to treat irrational numbers as algebraic objects the latter being made possible by the development of algebra. The real numbers are fundamental in calculus and more generally in all mathematics , in particular by their role in the classical definitions of limits , continuity and derivatives. Test your Knowledge on Real Numbers Q 5. Best Answer. There are also many ways to construct "the" real number system, and a popular approach involves starting from natural numbers, then defining rational numbers algebraically, and finally defining real numbers as equivalence classes of their Cauchy sequences or as Dedekind cuts, which are certain subsets of rational numbers. The ratio scale then segments by orders of magnitude used in science and technology, expressed in various units of measurement. See the figure, given below, which shows the classification of real numerals. Number systems. Contents move to sidebar hide. Foundations of Physics. All the positive real numbers are natural numbers.

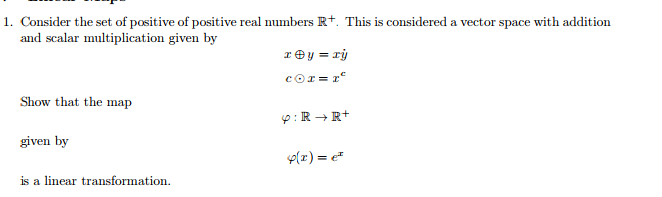
0 thoughts on “Positive real numbers”