Principal value of complex number
In mathematicsspecifically complex analysisthe principal values of a multivalued function are the values along one chosen branch of that functionso that it is single-valued. A simple case arises in taking the square root of a positive real number. Consider the complex logarithm function log z.
A complex number is an important section of mathematics as it is the combination of both real and imaginary elements. In the graphical representation, the horizontal line is used for the real numbers and the vertical lines is used to plot the imaginary numbers. Two concepts that come into the picture with the graphical representation of complex no. The modulus in mathematics is the square root of the summation of the squares of the real part plus the imaginary part of the complex number. On the other hand, the argument is the angle created with the positive direction of the real axis. With this article, we will learn about the argument of complex number formulas with the definition, solved examples and properties. The complex plane is similar to the cartesian plane and illustrates a geometric interpretation of complex numbers.
Principal value of complex number
By convention the positive real axis is drawn pointing rightward, the positive imaginary axis is drawn pointing upward, and complex numbers with positive real part are considered to have an anticlockwise argument with positive sign. When any real-valued angle is considered, the argument is a multivalued function operating on the nonzero complex numbers. The names magnitude , for the modulus, and phase , [3] [1] for the argument, are sometimes used equivalently. Similarly, from the periodicity of sin and cos , the second definition also has this property. The argument of zero is usually left undefined. Because it's defined in terms of roots , it also inherits the principal branch of square root as its own principal branch. This represents an angle of up to half a complete circle from the positive real axis in either direction. The principal value sometimes has the initial letter capitalized, as in Arg z , especially when a general version of the argument is also being considered. Note that notation varies, so arg and Arg may be interchanged in different texts. The set of all possible values of the argument can be written in terms of Arg as:. If a complex number is known in terms of its real and imaginary parts, then the function that calculates the principal value Arg is called the two-argument arctangent function, atan2 :.
Let us now proceed to understand how to determine the argument of complex numbers with an example and detailed steps. If you are checking Argument of Complex Number article, also check the related maths articles in the table below: Real numbers Decimal to hexadecimal conversion xl roman numerals cxxv roman numerals Prime numbers 1 to Less than. Retrieved
By convention the positive real axis is drawn pointing rightward, the positive imaginary axis is drawn pointing upward, and complex numbers with positive real part are considered to have an anticlockwise argument with positive sign. When any real-valued angle is considered, the argument is a multivalued function operating on the nonzero complex numbers. The names magnitude , for the modulus, and phase , [3] [1] for the argument, are sometimes used equivalently. Similarly, from the periodicity of sin and cos , the second definition also has this property. The argument of zero is usually left undefined.
The imaginary unit number is used to express the complex numbers, where i is defined as imaginary or unit imaginary. We will explain here imaginary numbers rules and chart, which are used in Mathematical calculations. The basic arithmetic operations on complex numbers can be done by calculators. The imaginary number i is also expressed as j sometimes. Basically the value of imaginary i is generated, when there is a negative number inside the square root, such that the square of an imaginary number is equal to the root of But when we take the cube of i, the value is -i. The imaginary number, when multiplied by itself, gives a negative value. For example, consider an imaginary number 3 i , if multiplied by itself or if we take the square of 3 i , gives 9 i 2 or we can write it as Also, 0 is considered as both the real number and an imaginary number.
Principal value of complex number
Before we get into the alternate forms we should first take a very brief look at a natural geometric interpretation of complex numbers since this will lead us into our first alternate form. An example of this is shown in the figure below. Note as well that we can now get a geometric interpretation of the modulus.
Builder hall 4 base link
More Articles for Maths. Download as PDF. The principal value sometimes has the initial letter capitalized, as in Arg z , especially when a general version of the argument is also being considered. We have examined the logarithm function above, i. Hidden categories: Articles with short description Short description is different from Wikidata. User page tools. Collins Dictionary 2nd ed. To determine the arg z value, fetch the real and imaginary components and substitute the values in the formula. Step 1: For the given complex no. Hence for any complex number z ,. Beardon, Alan
In mathematics , specifically complex analysis , the principal values of a multivalued function are the values along one chosen branch of that function , so that it is single-valued.
More More. Wiki tools Wiki tools Special pages Cite this page. Anonymous Not logged in Create account Log in. Hidden categories: Articles with short description Short description matches Wikidata Articles needing additional references from March All articles needing additional references. Because it's defined in terms of roots , it also inherits the principal branch of square root as its own principal branch. Now, for example, say we wish to find log i. Categories : Trigonometry Complex analysis Signal processing. Real numbers. Last updated on May 5, Contents move to sidebar hide. The set of all possible values of the argument can be written in terms of Arg as:. Home Maths Argument of Complex Numbers. The argument of zero is usually left undefined.

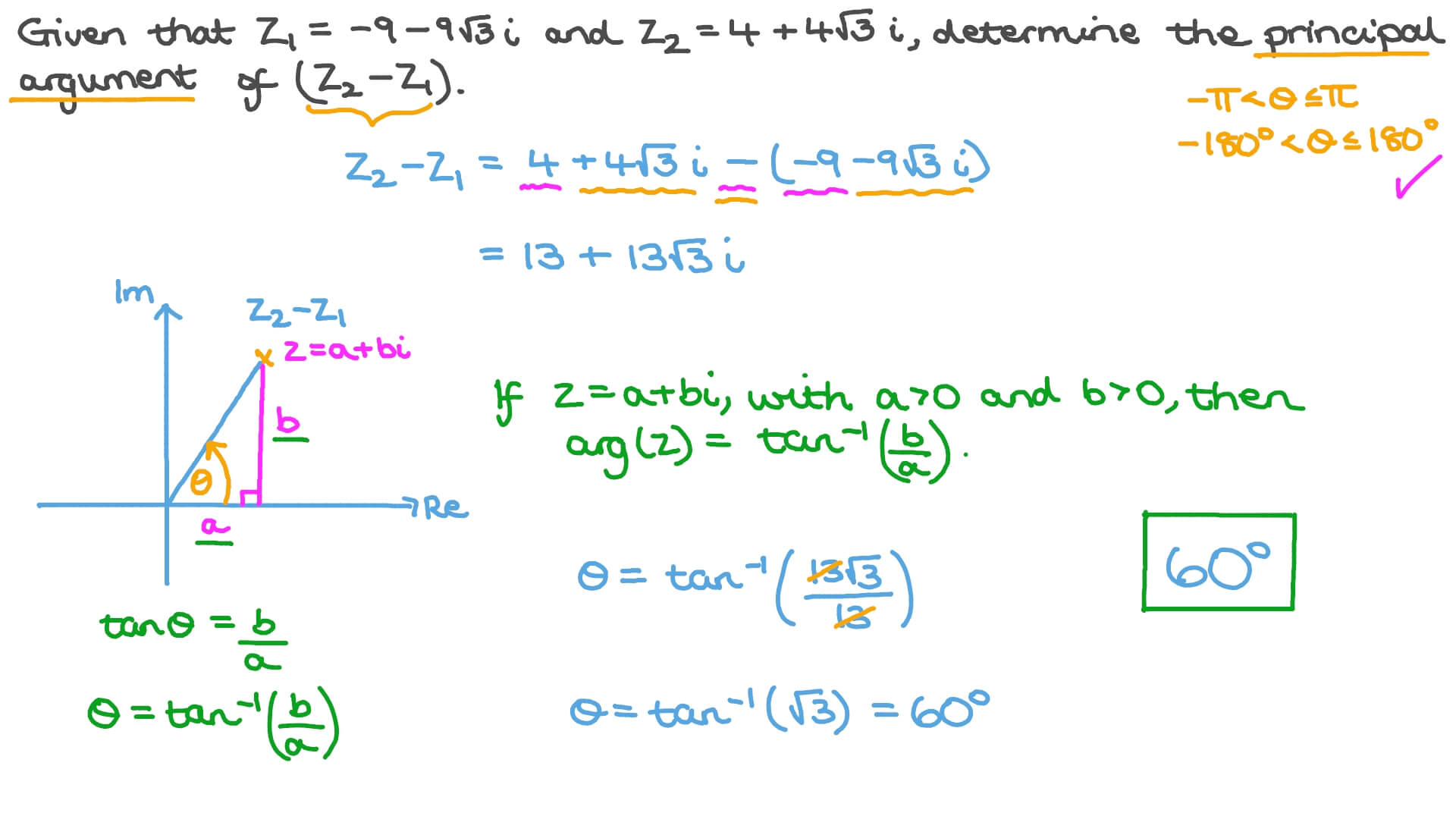
On mine it is very interesting theme. Give with you we will communicate in PM.
Excuse, I have removed this phrase
I consider, that you are not right. Let's discuss it. Write to me in PM.