Quadratic spline interpolation calculator
In the mathematical field of numerical analysis, spline interpolation is a form quadratic spline interpolation calculator interpolation where the interpolant is a special type of piecewise polynomial called a spline. You can read the full article of the spline interpolation on wiki.
Syntax for entering a set of points: Spaces separate x- and y-values of a point and a Newline distinguishes the next point. Hit the button Show example to see a demo. By default, the algorithm calculates a "natural" spline. Details about the mathematical background of this tool and boundary conditions can be found here. Cubic spline interpolation is a mathematical method commonly used to construct new points within the boundaries of a set of known points.
Quadratic spline interpolation calculator
This technique offers several advantages over other techniques. It produces a smooth curve over the interval being studied while at the same time offering a distinct polynomial for each subinterval known as Splines. Secondly it eliminates some of the problems inherent in trying fit a single higher order polynomial which can actually produce misleading estimates by being too precise. Fortunately, many applications including most spreadsheet programs allow us to solve the resulting system, easily producing the family of equations. The matrix operations are shown as well. Instead of one equation we could have an equation representing the interval [2,5] and a second equation [5,7]. The key is that the point in the middle contributes to both equations creating a connection that ensures a smooth handoff from the first to the second equation. The general form is:. Since we want to solve for the six constants in a proper linear fashion, we need four more equations. Since each equation satisfies two endpoints this allows us to double the number of equations as follows:.
So we can calculate b1 and b2 from them. Latest commit. The orange dots are the four closest interpolated values produced by the resulting cubic polynomial.
.
This technique offers several advantages over other techniques. It produces a smooth curve over the interval being studied while at the same time offering a distinct polynomial for each subinterval known as Splines. Secondly it eliminates some of the problems inherent in trying fit a single higher order polynomial which can actually produce misleading estimates by being too precise. Fortunately, many applications including most spreadsheet programs allow us to solve the resulting system, easily producing the family of equations. The matrix operations are shown as well. Instead of one equation we could have an equation representing the interval [2,5] and a second equation [5,7]. The key is that the point in the middle contributes to both equations creating a connection that ensures a smooth handoff from the first to the second equation. The general form is:. Since we want to solve for the six constants in a proper linear fashion, we need four more equations.
Quadratic spline interpolation calculator
This phenomenon was illustrated by Runge when he interpolated data based on a simple function of. It, however, did do a better job of approximating the data but except near the ends where the approximation is worse than before. So, what is the solution to using information from more data points, but at the same time keeping the function reasonably true to the data behavior? The answer is in spline interpolation and will be discussed in the following lessons. The most common types of spline interpolation used are linear, quadratic, and cubic. Summary : Learn via Runge's phenomena why higher-order interpolation is a bad idea.
Skyrim light vs heavy armor
Secondly it eliminates some of the problems inherent in trying fit a single higher order polynomial which can actually produce misleading estimates by being too precise. Quadratic spline interpolation. Below shows the setup using Matrix math to solve the cubic polynomial in a spreadsheet program. Since we often only want to look at a limited range the benefits of a significant reduction in algebraic manipulation outweighs the limitation. As we can see we need one more equation to define a,b, and c for every quadratic equation. Since each equation satisfies two endpoints this allows us to double the number of equations as follows:. From Eq2 into Eq1 :. The dotted line demonstrates that the cubic interpolation polynomial is less accurate as you move away from the four closest points. You switched accounts on another tab or window. This results in:. Go to file. From the same steps but by using sin theta we can conclude that:.
.
The general form is:. Other uses include the design of computer fonts and animation. These new points are function values of an interpolation function referred to as spline , which itself consists of multiple cubic piecewise polynomials. So actually after that another assumption we need 3n - 1 equations, and we already have those equations. The line graph shows in blue the actual measured data points. The sixth equation is based on the assumption that the line leaving the endpoint is a straight line. The matrix operations are shown as well. What if we assumed that the first equation is a linear equation? Toggle navigation. Branches Tags.

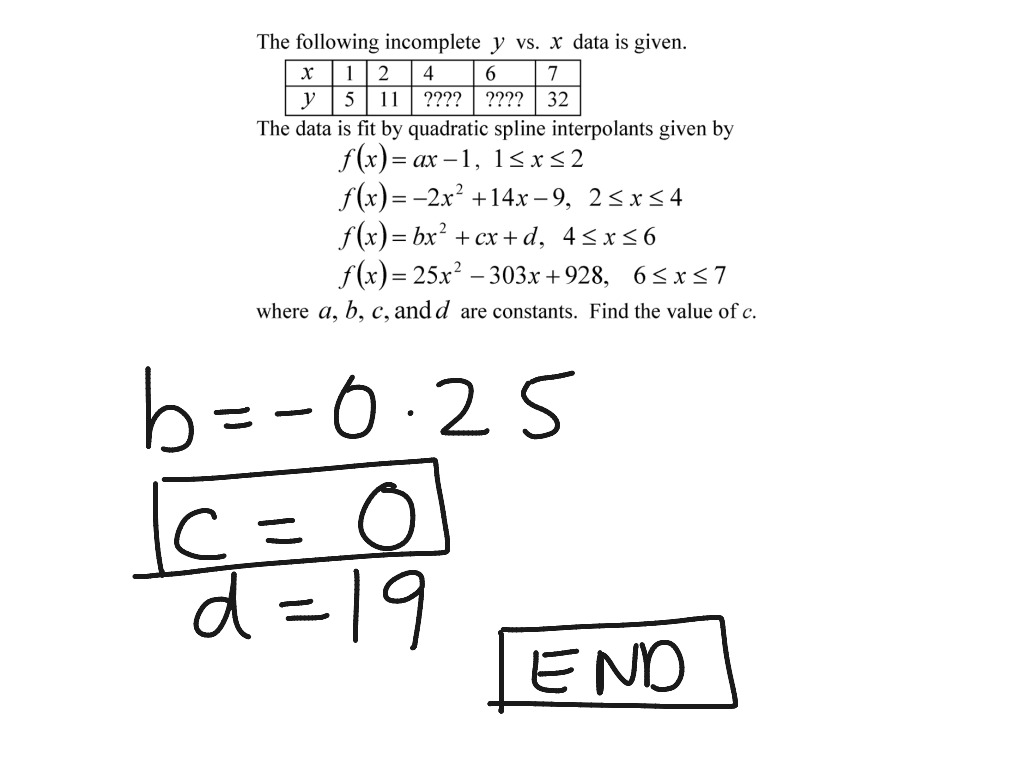
0 thoughts on “Quadratic spline interpolation calculator”