Solve bvp
Before we start off this section we need to make it very clear that we are only going to scratch the surface of the topic of boundary value solve bvp. There is enough material in the topic of boundary value problems that we could devote a whole class to it, solve bvp. The intent of this section is to give a brief and we mean very brief look at the idea of boundary value problems and to give enough information to allow us to do some basic partial differential equations in the next chapter.
The shooting method works by considering the boundary conditions as a multivariate function of initial conditions at some point, reducing the boundary value problem to finding the initial conditions that give a root. The advantage of the shooting method is that it takes advantage of the speed and adaptivity of methods for initial value problems. The disadvantage of the method is that it is not as robust as finite difference or collocation methods: some initial value problems with growing modes are inherently unstable even though the BVP itself may be quite well posed and stable. The shooting method looks for initial conditions so that. Since you are varying the initial conditions, it makes sense to think of as a function of them, so shooting can be thought of as finding such that.
Solve bvp
Help Center Help Center. This example shows how to use bvp4c to solve a boundary value problem with an unknown parameter. However, this only determines y x up to a constant multiple, so a third condition is required to specify a particular solution,. You can either include the required functions as local functions at the end of a file as done here , or save them as separate, named files in a directory on the MATLAB path. Create a function to code the equations. Note: All functions are included as local functions at the end of the example. Now, write a function that returns the residual value of the boundary conditions at the boundary points. In this form the boundary conditions are. Lastly, create an initial guess of the solution. Only eigenvalues and eigenfunctions that are close to the initial guesses can be computed. To increase the likelihood that the computed eigenfunction corresponds to the fourth eigenvalue, you should choose an initial guess that has the correct qualitative behavior.
For nonlinear problems, let be the Jacobian for the nonlinear Solve bvp system, and let be the Jacobian of the th boundary condition.
Help Center Help Center. This example uses bvp4c with two different initial guesses to find both solutions to a BVP problem. You either can include the required functions as local functions at the end of a file as done here , or save them as separate, named files in a directory on the MATLAB path. Create a function to code the equation. These inputs are automatically passed to the function by the solver, but the variable names determine how you code the equations. In this case, you can rewrite the second-order equation as a system of first-order equations.
The pycse book. The pycse blog. Adapted from Example 8. This is a boundary value problem not an initial value problem. First we consider using a finite difference method. We discretize the region and approximate the derivatives as:.
Solve bvp
Help Center Help Center. Use the bvpinit function to create the initial guess solinit , which also defines the points at which the boundary conditions in bcfun are enforced. For example, use the AbsTol and RelTol options to specify absolute and relative error tolerances, or the FJacobian option to provide the analytical partial derivatives of odefun. For this example, use the second-order equation. To solve this equation in MATLAB, you need to write a function that represents the equation as a system of first-order equations, a function for the boundary conditions, and a function for the initial guess. Then the BVP solver uses these three inputs to solve the equation.
Framing garage door
Listed here are the local helper functions that the BVP solver bvp4c calls to calculate the solution. So, by using this differential equation almost exclusively we can see and discuss the important behavior that we need to discuss and frees us up from lots of potentially messy solution details and or messy solutions. Note that the solution to system 3 is nontrivial because the first component of is always 1. Shooting from , the "Shooting" method gives warning messages about an ill-conditioned matrix and that the boundary conditions are not satisfied as well as they should be. While the Jacobian can be computed using finite differences, the sensitivity of solutions of an initial value problem IVP to its initial conditions may be too much to get reasonably accurate derivative values, so it is advantageous to compute the Jacobian as a solution to ODEs. Code Equation Create a function to code the equations. When you give NDSolve a problem that has no solution, numerical error may make it appear to be a solvable problem. As time permits I am working on them, however I don't have the amount of free time that I used to so it will take a while before anything shows up here. Off-Canvas Navigation Menu Toggle. This, however, is not possible and so in this case have no solution. Using 5 and replacing , and thinking of in terms of the other components of , you get the nonlinear equation.
Before we start off this section we need to make it very clear that we are only going to scratch the surface of the topic of boundary value problems.
This example shows how to use bvp4c to solve a boundary value problem with an unknown parameter. In this case, it is not able to integrate over the entire interval because of nonexistence. Example 6 Solve the following BVP. Call bvpinit to generate an initial guess of the solution. You have a modified version of this example. Then computation of for the linearized system gives the Jacobian for the nonlinear system for a particular initial condition, leading to a Newton iteration,. Once the initial conditions are determined, the usual methods for solving initial value problems can be applied. Go To Notes Practice and Assignment problems are not yet written. In each of the examples, with one exception, the differential equation that we solved was in the form,. Only eigenvalues and eigenfunctions that are close to the initial guesses can be computed. Example 8 Solve the following BVP.

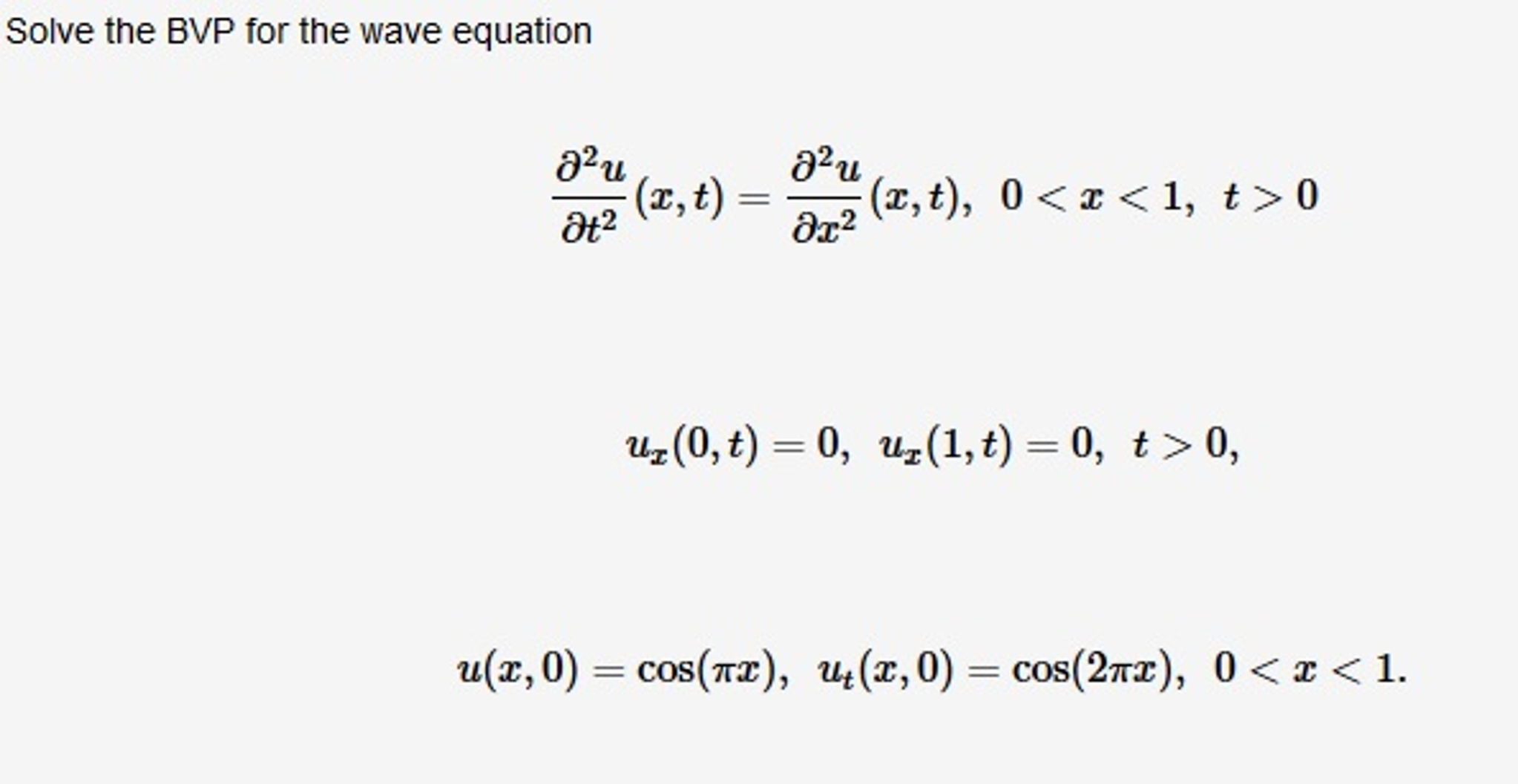
I with you completely agree.