Eigen matrixxd
The Matrix class is the work-horse for all dense note matrices and vectors within Eigen.
This is a very short guide on how to get started with Eigen. It has a dual purpose. It serves as a minimal introduction to the Eigen library for people who want to start coding as soon as possible. You can also read this page as the first part of the Tutorial, which explains the library in more detail; in this case you will continue with The Matrix class. In order to use Eigen , you just need to download and extract Eigen 's source code see the wiki for download instructions. In fact, the header files in the Eigen subdirectory are the only files required to compile programs using Eigen.
Eigen matrixxd
The Eigen library is divided in a Core module and several additional modules. Each module has a corresponding header file which has to be included in order to use the module. The Dense and Eigen header files are provided to conveniently gain access to several modules at once. Recall: Eigen provides two kinds of dense objects: mathematical matrices and vectors which are both represented by the template class Matrix , and general 1D and 2D arrays represented by the template class Array :. All combinations are allowed: you can have a matrix with a fixed number of rows and a dynamic number of columns, etc. The following are all valid:. In most cases, you can simply use one of the convenience typedefs for matrices and arrays. Some examples:. In the rest of this document we will use the following symbols to emphasize the features which are specifics to a given kind of object:. For instance:. In addition to the aforementioned operators, Eigen supports numerous coefficient-wise operator and functions. The following operators are readily available for arrays, or available through.
In the case of a compile-time column vector, implicit transposition from a single row is allowed. However if you think you don't need it, you can directly use the classes documentation and our Quick reference guide. Matrix3f a 3,3 ;, eigen matrixxd.
The Matrix class is the work-horse for all dense note matrices and vectors within Eigen. Vectors are matrices with one column, and row-vectors are matrices with one row. The Matrix class encompasses both fixed-size and dynamic-size objects note. The first three template parameters are required: The remaining template parameters are optional — in most cases you don't have to worry about them. Eigen provides a number of typedefs covering the usual cases. Here are some examples:.
In Eigen , all matrices and vectors are objects of the Matrix template class. Vectors are just a special case of matrices, with either 1 row or 1 column. The Matrix class takes six template parameters, but for now it's enough to learn about the first three first parameters. The three remaining parameters have default values, which for now we will leave untouched, and which we discuss below. The three mandatory template parameters of Matrix are:. We offer a lot of convenience typedefs to cover the usual cases. For example, Matrix4f is a 4x4 matrix of floats. Here is how it is defined by Eigen :.
Eigen matrixxd
This page discusses several advanced methods for initializing matrices. It gives more details on the comma-initializer, which was introduced before. It also explains how to get special matrices such as the identity matrix and the zero matrix.
Mhsindiana com rewards
Vectors are matrices with one column, and row-vectors are matrices with one row. MatrixXf m rows,cols ;. MatrixXf b 3,3 ;. This makes sense for very small matrices, typically up to 4x4, sometimes up to 16x In the general case, the constructor takes a list of rows, each row being represented as a list of coefficients:. This Matrix class handles dense, not sparse matrices and vectors. Includes Dense and Sparse header files the whole Eigen library. One of the most attractive features of the Eigen library is that it includes expression objects and lazy evaluation. To compute the coefficient-wise exponential use ArrayBase::exp. We will be exploring many of them over subsequent articles. This is unlike Sparse matrices and vectors where the coefficients are stored as a list of nonzero coefficients. Such a matrix is called a null matrix.
This is a very short guide on how to get started with Eigen. It has a dual purpose.
MatrixXi M 3,3 ;. How to "install" Eigen? In the general case of matrices and vectors with either fixed or runtime sizes, coefficients have to be grouped by rows and passed as an initializer list of initializer list details :. Vector4d c 5. Eigenvalues can also be calculated in an optimised manner. Here is an example of usage:. Maximum number of rows. Eigen 3. As an example, an expression such as:. By spending months optimising a custom library, you are neglecting the original intent of its usage of the first place - solving quant problems! The use of fixed-size matrices and vectors has two advantages. Constructs an uninitialized matrix with rows rows and cols columns. Writing our own matrix libraries is likely to cause a few issues in a production environment: Poor Performance - Unless significant time is spent optimising a custom matrix library, it is often going to be far slower than the corresponding dedicated community projects such as uBLAS , Eigen or Blitz. Maximum number of columns. The benefit of such an approach is that most compilers are able to heavily optimise the expression such that additional loops are completely minimised.

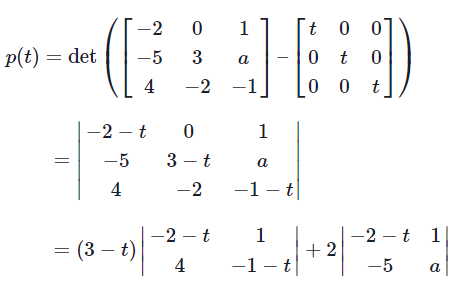
It is rather valuable piece
I protest against it.