World hardest maths sum
Well, m aybe. For now, you can take a crack at the hardest math problems known to man, woman, and machine.
Advanced Math Robotics. Schedule a Free Class. Update : This article was last updated on 12th Oct to reflect the accuracy and up-to-date information on the page. The mystical world of mathematics—is home to confounding problems that can make even the most seasoned mathematicians scratch their heads. Problem : Can every map be colored with just four colors so that no two adjacent regions have the same color?
World hardest maths sum
Suggestions or feedback? Images for download on the MIT News office website are made available to non-commercial entities, press and the general public under a Creative Commons Attribution Non-Commercial No Derivatives license. You may not alter the images provided, other than to crop them to size. A credit line must be used when reproducing images; if one is not provided below, credit the images to "MIT. Previous image Next image. What do you do after solving the answer to life, the universe, and everything? In , Booker, at the University of Bristol, and Sutherland, principal research scientist at MIT, were the first to find the answer to In mathematics, entirely by coincidence, there exists a polynomial equation for which the answer, 42, had similarly eluded mathematicians for decades. When the sum of cubes equation is framed in this way, for certain values of k, the integer solutions for x, y, and z can grow to enormous numbers. The number space that mathematicians must search across for these numbers is larger still, requiring intricate and massive computations. Over the years, mathematicians had managed through various means to solve the equation, either finding a solution or determining that a solution must not exist, for every value of k between 1 and — except for In September , Booker and Sutherland, harnessing the combined power of half a million home computers around the world, for the first time found a solution to The widely reported breakthrough spurred the team to tackle an even harder, and in some ways more universal problem: finding the next solution for 3. Booker and Sutherland have now published the solutions for 42 and 3, along with several other numbers greater than , this week in the Proceedings of the National Academy of Sciences. Finding a third solution, however, has stumped expert number theorists for decades, and in the puzzle prompted pioneering mathematician Louis Mordell to ask the question: Is it even possible to know whether other solutions for 3 exist?
Search Search.
In , mathematicians finally solved one of the hardest math problems —one that had stumped them for decades. On the surface, it seems easy. That turned out to be much harder—as in, no one was able to solve for those integers for 65 years until a supercomputer finally came up with the solution to So here are nine more brutally difficult math problems that once seemed impossible, until mathematicians found a breakthrough. In some significant sense, a ball is the simplest of these shapes. It was groundbreaking, yet modest. Perelman rejected both.
The Millennium Prize Problems are seven well-known complex mathematical problems selected by the Clay Mathematics Institute in Thus, on the official website of the Clay Mathematics Institute, these seven problems are officially called the Millennium Problems. However, he declined the award as it was not also offered to Richard S. Hamilton , upon whose work Perelman built. The Clay Institute was inspired by a set of twenty-three problems organized by the mathematician David Hilbert in which were highly influential in driving the progress of mathematics in the twentieth century. Unlike Hilbert's problems, the problems selected by the Clay Institute were already renowned among professional mathematicians, with many actively working towards their resolution. His refusal of the Clay Institute's monetary prize in was widely covered in the media. The other six Millennium Prize Problems remain unsolved, despite a large number of unsatisfactory proofs by both amateur and professional mathematicians. Some mathematicians have been more critical.
World hardest maths sum
Suggestions or feedback? Images for download on the MIT News office website are made available to non-commercial entities, press and the general public under a Creative Commons Attribution Non-Commercial No Derivatives license. You may not alter the images provided, other than to crop them to size. A credit line must be used when reproducing images; if one is not provided below, credit the images to "MIT. Previous image Next image. What do you do after solving the answer to life, the universe, and everything? In , Booker, at the University of Bristol, and Sutherland, principal research scientist at MIT, were the first to find the answer to In mathematics, entirely by coincidence, there exists a polynomial equation for which the answer, 42, had similarly eluded mathematicians for decades. When the sum of cubes equation is framed in this way, for certain values of k, the integer solutions for x, y, and z can grow to enormous numbers.
8 am ist to est
Two mathematicians at the University of Illinois, Urbana-Champaign, Kenneth Appel and Wolfgang Hakan, found a way to reduce the proof to a large, finite number of cases. Well, m aybe. Mathematicians have slowly whittled the possibilities to fairly narrow ranges for up to 24 dimensions, with a few exactly known, as you can see on this chart. Riemann developed them while studying prime numbers and their distribution. Caption :. Over the years, mathematicians had managed through various means to solve the equation, either finding a solution or determining that a solution must not exist, for every value of k between 1 and — except for Since then, the proof has been a popular target for rewrites, enjoying many cosmetic revisions and simplifications. In some significant sense, a ball is the simplest of these shapes. What do you do after solving the answer to life, the universe, and everything? Oldest Newest Most Voted. These are known as the Pythagorean Triples, like 3,4,5 and 5,12, One of the greatest unsolved mysteries in math is also very easy to write.
SAT Math. Want to test yourself against the most difficult SAT math questions? Want to know what makes these questions so difficult and how best to solve them?
Previous image Next image. It was groundbreaking, yet modest. The digit solution to the decades-old problem suggests many more solutions exist. Problem : There are no three positive integers a,b,c that satisfies. But we need proof for all natural numbers. You may have heard of the Axiom of Choice, another independent statement. But the impact of the theorem has only grown. Updated: August 31, This was their idea: Trouble proving there are infinitely many primes with a difference of 2? With computer assistance, they exhaustively checked the nearly 2, cases, and ended up with an unprecedented style of proof. I mean I get exhausted and start panicking.

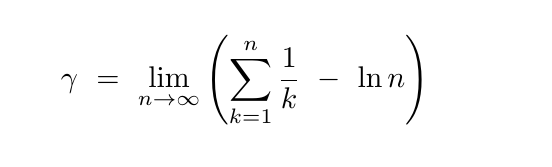
Useful phrase
I believe, that always there is a possibility.